1. GENERATORI CONTROLLATI
Controlled Generators

a) Generatore di tensione controllato in tensione
b) Generatore di tensione controllato in corrente
c) Generatore di corrente controllato in corrente
d) Generatore di corrente controllato in tensione.
Come casi speciali di Generatori Controllati, possiamo definire i seguenti:

a) Convertitore tensione-tensione
b) Convertitore corrente-tensione
c) Convertitore corrente-corrente
d) Convertitore tensione-corrente
Un'altra classe importante di generatori controllati è: e) box di isolamento, o buffer,
in cui la tensione di uscita è uguale alla tensione di ingresso ma la corrente di ingresso è nulla.

2. DIODI DI CHUA
Chua's Diodes
Se un resistore a due terminali è caratterizzato da una curva nel piano  i/V
diversa da una linea retta passante per l'origine, esso si chiama resistore
non lineare o Diodo di Chua. Vi sono due tipi di diodi di Chua:

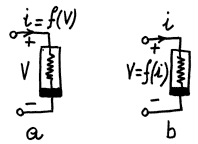
a) Diodo di Chua controllato in tensione, in cui i = f(V)
b) Diodo di Chua controllato in corrente, in cui V = f(i)
Notare che il tipo a) può essere considerato un generatore di corrente controllato
in tensione, mentre b) come un generatore di tensione controllato da una corrente.

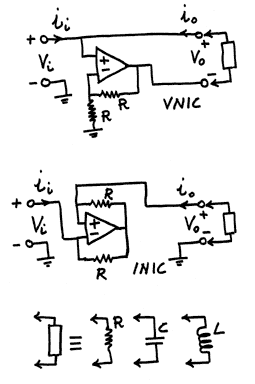
3. CONVERTITORI DI IMPEDENZE NEGATIVE
Negative-impedance converters
Questi generatori sono anche detti "Convertitori di impedenza a inversione di tensione"
o VNIC e "Convertitori di impedenza a inversione di corrente", o INIC.

Sono qui indicati i simboli del VNIC e del INIC, insieme ad una loro realizzazione
con amplificatori operazionali. Il VNIC ha l'effetto di riflettere la caratteristica
V-i attorno all'asse delle i, invertendo quindi il segno della tensione, mentre il INIC
riflette la caratteristica V-i attorno all'asse delle V, invertendo quindi il segno della
corrente.
Se un Diodo di Chua è collegato alla porta di destra di un VNIC, la porta di ingresso
si comporterà come un resistore non-lineare negativo di caratteristica i = - f(V).
In più, se un capacitore lineare di dinamica C(dV/dt) = i o un induttore lineare
di dinamica L(dV/dt) = V vengono collegati alla porta di destra di un VNIC, la porta
di sinistra si comporterà come un capacitore negativo di dinamica -C(dV/dt) = i,
o come un induttore negativo di dinamica -L(di/dt) = V, rispettivamente. Situazioni
simmetricamente identiche con gli INIC.
Riassumendo:

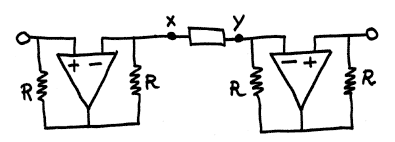
Occorre notare che nelle realizzazioni circuitali indicate uno dei terminali
del componente negativo sintetizzato è a massa. Se occorre che il componente
sia flottante, si ha questa possibile soluzione:

Oppure la seguente:

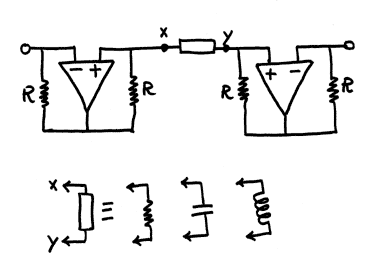
Questo secondo circuito è semplicemente ottenuto collegando in serie due
INIC non flottanti, mentre il primo dischiude interessanti possibilità di
trasformazioni per simmetrie.

4. CONVERTITORI DI IMPEDENZA
GENERALIZZATI
General Impedance Converters (GIC's)
Questi circuiti sono estremamente utili quando occorra sintetizzare elementi
di circuito di valore particolare e preciso, oppure di valore variabile entro
larghissimi limiti. La teoria è complessa, ma agli effetti pratici si veda il seguente
circuito generale, noto anche come Giratore:

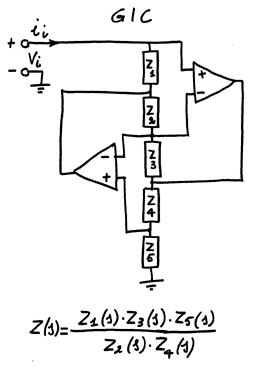
Per esempio, ponendo Z₁ = R₁,  Z₂ = R₂,  Z₃ = R₃,  Z₄ = R₄ e  Z₅ = 1/sC, otteniamo
un capacitore ideale di impedenza Z(s) = (R₁ R₃)/(s C R₂ R₄), ovvero di capacità
C = (R₁ R₃)/(C R₂ R₄), come nell'esempio seguente:

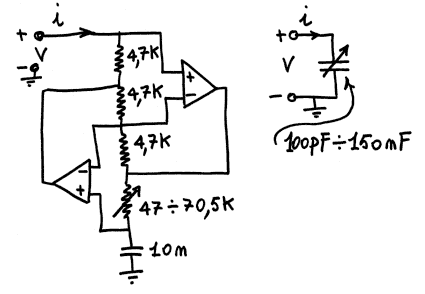
dove, variando Z₄ = R₄ si ottiene un circuito che si comporta come un capacitore
ideale variabile nel rapporto 1 : 1000 per semplice variazione di una resistenza,
cosa irrealizzabile altrimenti. Analogamente, il circuito seguente:

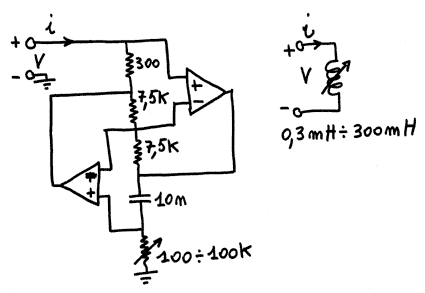
si comporta anch'esso come un induttore ideale  variabile nel rapporto 1:1000
per semplice variazione di una resistenza.
Ancora: ponendo Z₁ = 1/sC1,  Z₂ = R₂, Z₃ = R₃,  Z₄ = R₄  e Z₅ = 1/sC₅ , si ottiene
un resistore negativo dipendente dalla frequenza (FDNR) di impedenza
Z(s) = R₃/(s² C₁ C₅ R₂ R₄) = 1/a s² , dove a = (C₁ C₅ R₂ R₄)/R₃. Di conseguenza
se tutti i componenti sono reali la sua dinamica è:  a(d²V/dt²) = i, e l'impedenza
varia in proporzione inversa con il quadrato della frequenza.
Se occorre realizzare un elemento di circuito flottante, si usa la seguente
disposizione circuitale:

con gli stessi ruoli degli impedori nei  circuiti precedenti.

5. APPLICAZIONI AI CIRCUITI OSCILLATORI CAOTICI
Chaotic Oscillator applications

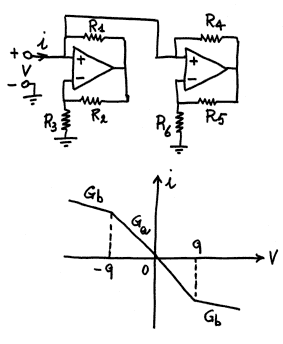
Due INIC (visti al paragrafo 3) con diversi valori della resistenza negativa
(-R₃ e -R₆) connessi semplicemente in parallelo costituiscono il cuore del
fondamentale circuito oscillatore caotico di Chua.
I parametri della caratteristica i-V riportata sono i seguenti:
Ga = - R₃^-1 - R₆^-1;
Gb = - R₃^-1 + R₄^-1
q = (R₅ E_sat)/(R₅ + R₆),
dove E_sat è la tensione di saturazione del secondo amplificatore operazionale.
Questo circuito è il tipico "Diodo di Chua", realizzato con un amplificatore
operazionale doppio TL082. Nel TL082 alimentato fra + 15 V e - 15 V la tensione
di saturazione è esattamente: E_sat =  14 V. Un esempio di circuito oscillatore
caotico di Chua  è riportato qui di seguito:

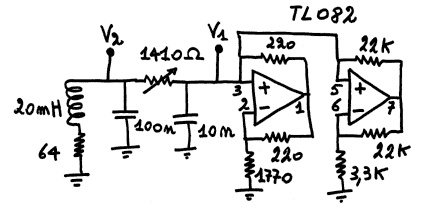
In questo circuito l'induttore può essere sintetizzato con un giratore secondo le linee
del paragrafo precedente, vedi anche G. Pegna, R. Marrocu, R. Tonelli and F. Meloni,
"Experimental Definition of the Basin of Attraction for Chua's Circuit",
Int, J. of Bifurcation and Chaos 10, No.5 (2000) 959-970. Alcune forme d'onda che
si ottengono variando il resistore da 1410 Ohm sono riportate qui di seguito:

Queste configurazioni sono dette "attrattori", e sono visualizzazioni XY dei segnali V₁ e V₂
all'oscilloscopio.

6. QUALCHE APPLICAZIONE E QUALCHE PROBLEMA
INTERESSANTE
Interesting applications and problems

a) resistenze positive e negative in serie e in parallelo:
- Una resistenza negativa in parallelo ad una uguale resistenza positiva è un circuito aperto.
- Una resistenza negativa in serie ad una uguale resistenza positiva è un corto circuito.
b) Applicazioni dei giratori ai circuiti radio per ELF (frequenze ultra-basse): vedi.
c) Più interessanti sono le possibilità di annullare una capacità, per esempio
una capacità parassita, collegando in parallelo ad essa una uguale capacità negativa.
Ma sarebbe possibile avere capacità infinite con il collegamento in serie
di una capacità positiva con una uguale capacità negativa?
d) Analogamente: come si comporterebbe un induttore di valore infinito creato collegando
in parallelo due induttori di uguale valore ma di segno opposto?
e) Problemi da studiare: comportamento dinamico di circuiti -R-C  e di circuiti
-C-R  (R e C negativi).